Why are Merkle Trees Important in Blockchain?
**Please note: In this article, I purposely use the terms data snippet and transaction interchangably as I predict a future where Blockchain usage transcends well beyond crypto currencies.
Blockchain technology introduces various concepts and structures that help maintain a secure, distributed ledger. One such fundamental structure is the Merkle tree. Often referred to as a Hash Tree, a Merkle tree organizes and verifies large sets of data. In the case of blockchains, those datasets are typically transactions but could be any snippets of data. This post explains what a Merkle tree is, how it works in a blockchain, and why it is crucial for both security and efficiency.
What Is a Merkle Tree?
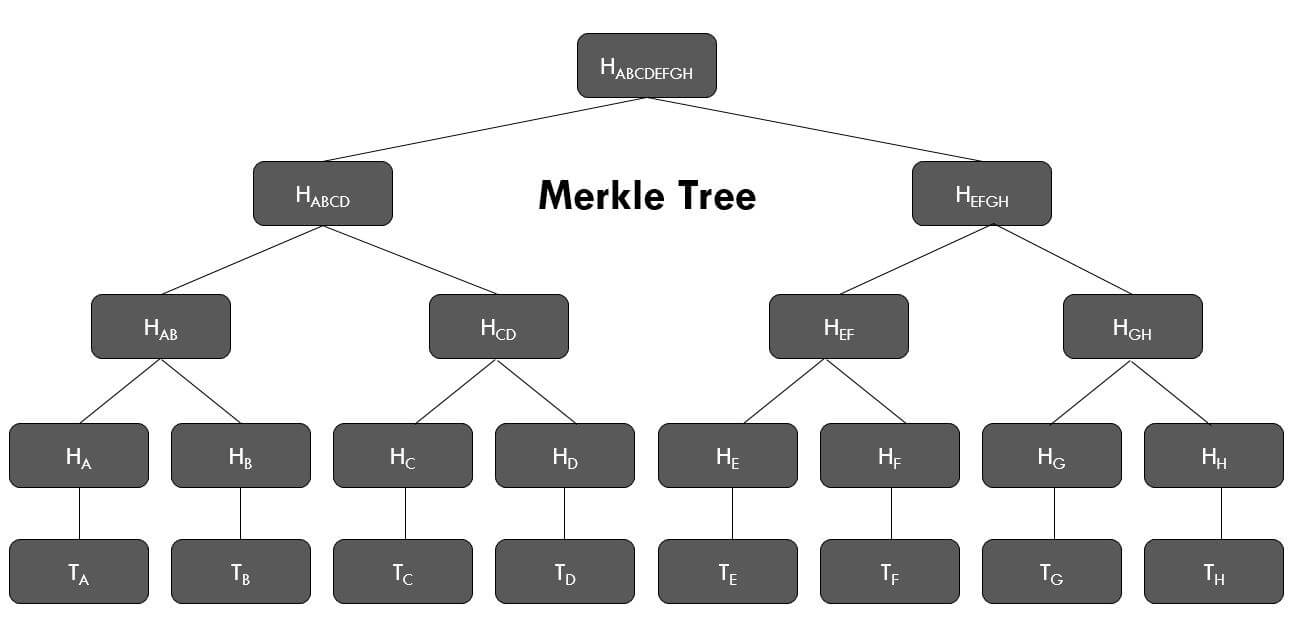
A Merkle tree is a binary tree where leaf nodes represent hashed data (such as crypto transactions), and each non-leaf node contains the hash of its two child nodes. Ultimately, there is a single hash at the top of the tree, known as the Merkle root, which uniquely represents all the data below it. This structure provides a concise summary of a large data set.
For instance, consider four Data Snippets (Dt1, Dt2, Dt3, Dt4). Each transaction is first hashed (H1 = Hash(Dt1), H2 = Hash(Dt2), and so on). These hashes form the leaves of the tree. Next, pairs of leaf hashes are combined and hashed again to form parent nodes. The process continues until only one hash remains, which is the Merkle root.
Benefits to the Blockchain
Merkle trees offer significant benefits for data integrity and verification. By placing the Merkle root in the block header, anyone can verify that specific data snippets are included in a block without having to download every other data snippet in that block. This is highly efficient for nodes with limited resources,often referred to as light nodes, because they can request just enough information, known as a Merkle proof, to check if a particular data snippet is valid and included.
If any data snippet is altered or a single bit changes within the block, its hash in the Merkle tree changes. This alteration cascades upward, ultimately changing the Merkle root. This hashing mechanism underpins the immutability and trustworthiness of blockchain data.
Building the Merkle Tree in a Block
In a blockchain, the Merkle tree is constructed each time a new block is proposed (usually by a miner or validator). Suppose a block contains N data snippets:
- Each data snippet is hashed individually.
- These hashes are paired, concatenated, and hashed again to create parent node hashes.
- The pairing and hashing process continues until there is only one hash left, which is the Merkle root.
- The resulting Merkle root is placed in the block header, alongside the previous block’s hash, a timestamp, a nonce, and other necessary data.
- The block data, including the Merkle root, is then hashed generating the block hash.
Verifying a Transaction with a Merkle Proof
One of the most powerful features of Merkle trees in blockchains is the ability to prove a transaction’s inclusion without downloading the entire block. This process, known as Merkle proof, works by providing the hashes along the path from the transaction’s leaf node up to the Merkle root. Each step in this path can be used to compute a parent hash, eventually reconstructing the root. If the computed root matches the one stored in the block header, it confirms that the transaction is indeed part of that block.
For example, if you want to verify Dt2 in a small block of four data snippets, the information needed includes Dt2’s hash, Dt1’s hash (to reconstruct the pair), and the hash of the sibling pair (Dt3 and Dt4’s combined hash). By iterating through these hashes, a verifier recalculates the Merkle root. If there is a match with the block’s recorded root, Dt2 is confirmed as part of the block.
Merkle Trees and Blockchain Security
Merkle trees maintain the integrity of block data and make tampering difficult. Any malicious change to a transaction triggers a mismatch in the Merkle root, rendering the block invalid unless the attacker redoes the necessary cryptographic proof. This design ensures that data tampering is immediately evident to honest nodes, reinforcing the blockchain’s immutability.
In addition to security, the use of Merkle trees greatly reduces the computing and bandwidth requirements for transaction verification. Nodes that do not store the entire blockchain, or light nodes, can still validate data snippets by relying on Merkle proofs. This capability broadens participation in the network, since even resource constrained devices can verify transactions securely.
References and Further Reading
-
Toshendra Kumar Sharma (2024). “Merkle tree in Blockchain”. Blockchain Council. https://www.blockchain-council.org/blockchain/what-is-merkel-tree-merkel-root-in-blockchain/
-
Ethereum Foundation. “Merkle Patricia Trie”. https://ethereum.org/en/developers/docs/data-structures-and-encoding/patricia-merkle-trie/
-
Till Antonio Mahler (2018). “Merkle Trees — Ensuring Integrity On Blockchains”. Medium. https://medium.com/blockwhat/merkle-trees-ensuring-integrity-on-blockchains-508d6647d58e
